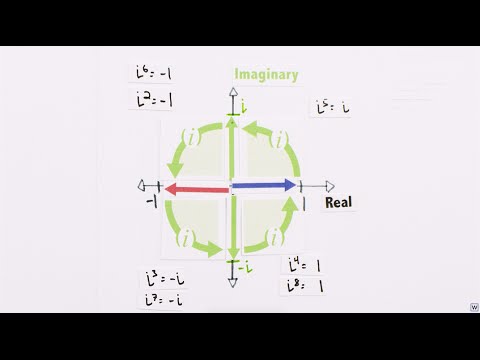
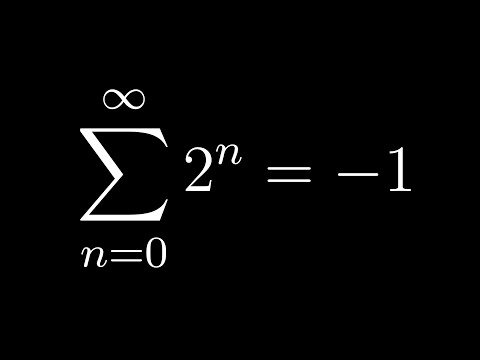For early access to new videos and other perks: Want to learn more or teach this series? Check out the Imaginary Numbers are Real Workbook: Imaginary numbers are not some wild invention, they are the deep and natural result of extending our number system. Imaginary numbers are all about the discovery of numbers existing not in one dimension along the number line, but in full two dimensional space. Accepting this not only gives us more rich and complete mathematics, but also unlocks a ridiculous amount of very real, very tangible problems in science and engineering. Part 1: Introduction Part 2: A Little History Part 3: Cardan's Problem Part 4: Bombelli's Solution Part 5: Numbers are Two Dimensional Part 6: The Complex Plane Part 7: Complex Multiplication Part 8: Math Wizardry Part 9: Closure Part 10: Complex Functions Part 11: Wandering in Four Dimensions Part 12: Riemann's Solution Part 13: Riemann Surfaces Thanks to viewer "David O" for this correction: The claim that Euler didn’t know what to do with negative numbers, or thought they were greater than infinity, is a misinterpretation of his On Divergent Series paper. Euler argued that, for infinite series, the word “sum” should mean the original finite expression from which the series originates. For example, applying the geometric series formula "1/(1–r) = 1 + r + r^2 + r^3 + …" with r = 2 gives the formal result "–1 = 1 + 2 + 4 + 8 + …”. However, he did not mean that negative numbers themselves are infinite, nor that such “sums” are equal in the ordinary arithmetic sense for divergent series. Source: Paragraphs 1-12 of Want to learn more or teach this series? Check out the Imaginary Numbers are Real Workbook: